Minh N. Do: Research
Research Output on Illinois Expert
ORCID (Open Researcher and Contributor ID)
Research Statement
Imaging was selected by the National Academy of Engineering as one of the
20 greatest engineering achievements of the 20th century. Imaging technologies
continue to have significant impacts on many aspects of our lives.
Everyday users access multimedia information on the Web. Doctors routinely rely
on medical images (such as MRI and CT scans) for diagnostics. Scientists use
images from very large scale (astronomical images) to understand the origin of
the universe to very small scale (molecular images) to understand how billions
of DNA molecules give rise to a human being.
This trend of increasing dependency on imaging technologies has created an
unprecedented demand for more powerful and effective image processing algorithms
and applications. At the fundamental level, traditional image processing has
largely been developed as a simple separable extension from the one-dimensional
signal processing. My primary research goal has been developing new "true"
multidimensional tools that can capture geometrical structures that
typically are the dominant feature in images and multidimensional data.
Geometric image representations and processing.
Efficient representation of visual information lies at the heart of many image
processing tasks such as reconstruction, compression, denoising, and feature
extraction. For example, a 512 by 512 color image can be considered as a point
in a 512*512*3 dimensional space (each pixel is represented by a triple of color
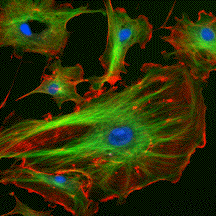
components). However, as we can see in the figure below, a randomly chosen
image from this space is far from being a "real" image. In other words, "real"
images live in tiny parts of the huge space of all possible images. Effectively
exploring this fact allows us to compress an image or to filter a clean image
out from contaminated noise.
 |
 |
 |
| A natural image |
A bioimage |
A random image |
As can be seen from the above figure, the key distinguishing feature of
"real" images is that they have intrinsic geometrical structure. In
particular, visual information is mainly contained in the geometry of object
boundaries. Although geometry has been long considered in mathematics and
computer vision for modeling visual information, the challenges in exploring
geometry in image processing come from the discrete nature of the data, as well
as the issues of robustness and efficiency. I am working on a
discrete-space framework for the construction of multiscale geometric
image transforms and algorithms that can be applied to sampled images. I plan
to use this as a stepping stone to bridge the gap between the low-level image
processing algorithms and the high-level geometry models in computer vision.
Furthermore, by connecting and unifying ideas from harmonic analysis, visual
perception, computer vision, and signal processing, I seek new fruitful
interactions between these fields.
Integrating image formation and image processing. On the
other side of the image processing world is image formation --
the process of forming an image from acquired data (e.g. generating a computer
tomography image from X-ray measurements). Typically, these two fields have
been developed independently using digital images as the link. To be more
effective, future imaging systems need to integrate all layers from image
formation to high level image processing.
Since images are formed and processed in digital form, at the heart of this
integration is the intersection between the continuous and discrete domains.
Traditionally, this is handled via the Shannon sampling theorem under the
bandlimited condition, which is typically violated by the existence of a
discontinuity. Consequently, it is of considerable interest to develop new
sampling and reconstruction schemes for more general image classes than the
usual bandlimited model. I am working toward a new sampling theory for
multidimensional signals that can be represented or approximated by a finite
number of parameters (e.g. piecewise smooth images with piecewise smooth
boundaries). Such sampling theory would lead to powerful image processing
algorithms that work directly with the acquired data.
Image processing and reconstruction from multiple sensors.
Existing visual recording systems use a single camera, and thus provide viewers
with a passive viewing experience. I envision the development of new systems
employing multiple cameras and sensors to deliver unprecedented immersive
recording and viewing capabilities. Such systems are expected to be feasible
thanks to the continuing improvement in digital technology that now offers
low-cost sensors and massive computing power.
In this direction, I am investigating new imaging techniques for
reconstruction of the visual recording at an arbitrary location in space and
time from multiple cameras and sensors. This can be seen as a sampling problem
of the high-dimensional plenoptic function that describes the light
intensity passing through every viewpoint, in every direction, for all time, and
for every wavelength. My main goal here is to search for new high-dimensional
representations and processing algorithms that can deal effectively with
plenoptic geometrical structures.
In summary, I am interested in developing new
multidimensional signal processing tools, and applying these tools to a wide
range of imaging applications. This work will require deep ideas in mathematics
and information theory, and will also combine notions from the physics of sensor
data, computer algorithms, and the psychology of perception. I have found that
performing research from pure theoretical investigations to practical
applications, especially where there is a cross feeding between theory and
practice as well as between different fields, is extremely productive.